Gear Module: Exploring Its Meaning and Function in Gears

Introduction

The gear module is a fundamental metric for determining tooth size and profile geometry. In the world of gear design, while the module is the primary standard for metric systems, it is intrinsically linked to gear pitch—another critical measure of tooth spacing. While many auxiliary parameters can be adjusted independently, the module remains the decisive factor that ensures compatibility between mating gears in any practical application.

In engineering practice, the module dictates part interchangeability, load-carrying capacity, and the overall footprint of the gear train. Regardless of manufacturing precision, an incorrect module selection will compromise mesh integrity and lead to structural failure under design loads. This article provides a clear definition of gear module components and examines why it remains a critical design parameter, influencing everything from mechanical strength and geometry to production efficiency and long-term reliability.

For readers unfamiliar with different gear measurement systems, our article "[What Is Gear Pitch?]" provides helpful context and complements the concept of gear module.

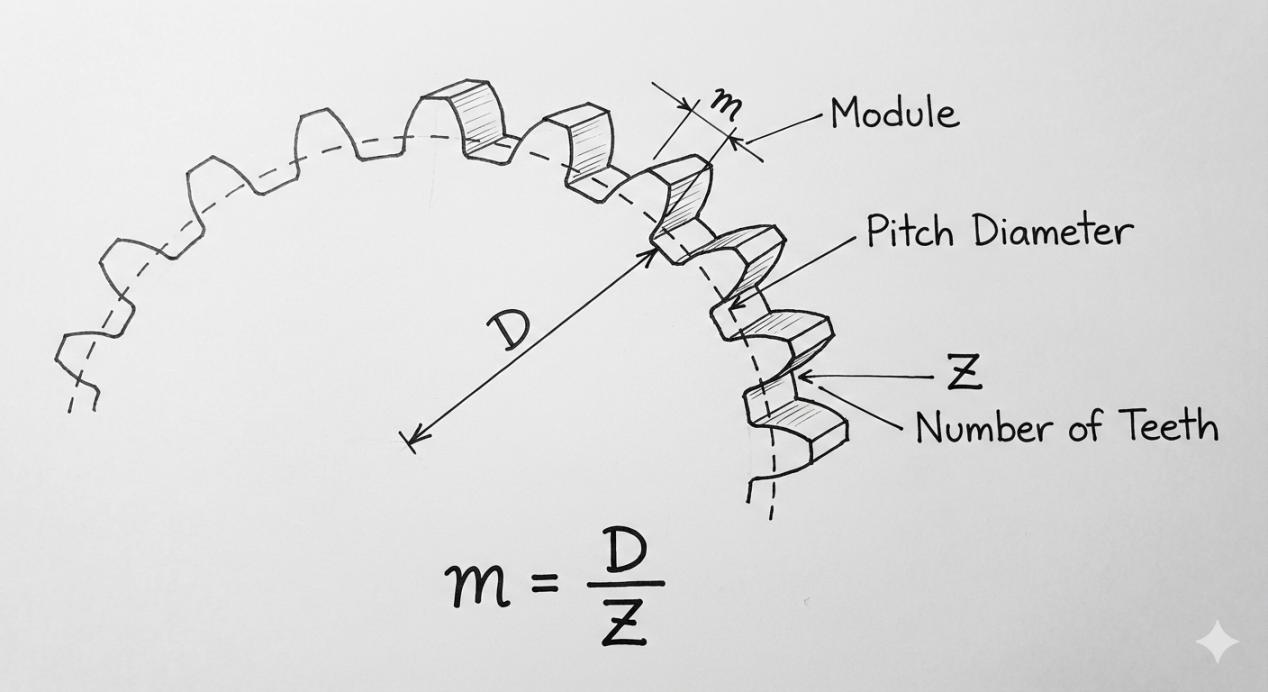
Defining the Core Parameter: What is a Gear Module?

To Construct the Module of a Gear

The gear module is a metric unit that defines the size of the gears' teeth. It is mathematically expressed as:

Module (m) = Pitch Diameter (D) / Number of Teeth (Z)

The module is a measure of gear size, which, because these gears are directly related to each other, means that it links the overall sizes of gears with their tooth counts. The larger the module, the bigger the teeth, and vice versa.

The gear module is all standard, so that there is no difference in the tooth form. Two gears with the same module and pressure angle will mesh properly. This standardization means module gear systems are interchangeable and dependable wherever in the world you may be.

Metric vs. Diametral Pitch (DP)

The metric gear system and module are the unit of size. Imperial gear system, power up transmission applied from this will be Diametral Pitch (DP). It is the number of teeth per inch of pitch diameter, which makes it reciprocal to module size.

More concretely, a small module corresponds to a large Diametral Pitch and vice versa. Conversion from one to the other is achievable, but gears of both systems cannot be combined with each other, and metric module gears should not mesh with DP gears without conversion.

Present-day worldwide production is immensely in favor of module gear trains, as this system complies with ISO and DIN standards protocols, which streamlines the globalization process.

Effect of Gear Module Parameters on the Tooth Forms

Tooth Size and Strength Determination by Module

The gear module has the most direct influence on tooth size. With an increase in module, the tooth thickens, deepens, and becomes mechanically more powerful. This greater capacity permits the gear to accept higher loads or increased tooth pinion sizes.

Conversely, a small gear module makes smaller and more precise teeth suitable for fine mechanics, but with less load-bearing capacity. This is why heavy machinery works with big modules, whereas instruments and actuators use small ones.

In other words, module order is a trade-off between compactness and strength. The right module of a gear allows the teeth to resist the transmitted torque without exhibiting wear or breaking.

Pitch Circle Diameter and Center Distance Affected by the Module

As soon as the module is chosen, it immediately sets or selects the pitch circle of the gear. Notice that because pitch diameter is module times teeth, any change in module scales the whole gear.

This also applies to the central distance of gears engaging each other. When the number of teeth is constant, going to a higher module requires a larger center distance. Therefore, the choice of module doesn't just affect the gears of a mechanical structure; it determines its overall architecture too.

Consequently, designers must consider space restrictions from the outset, as to change module at a later stage often necessitates redesign of shafts, housings, and bearings.

Standardization and Interchangeability

Why the Match Module Is Important for Gear Integration

To engage properly, two gears must have the same module of a gear. Even a small module error will result in improper teeth meshing and noise, vibration, wear, and part failure.

The matching module makes certain that the tooth space and tooth profile of one gear rotate exactly into synchronism with the carrying gear. This is the case regardless of whether a spur, helical, bevel, or internal gear is used.

Thanks to this hard rule, the module parameter is a no-compromising factor in gear matching or substitution.

Modules Conforming to Standards (ISO, DIN)

This is a standardized value of a module, as specified by international standards such as ISO and DIN. These series provide the convenience of choosing frequently used sizes instead of specifying custom dimensions.

The use of standard module gears enables universal replacement, simplifying the supply process and reducing costs. It also allows replacement gears to be secured fast with no redesign of the mating parts.

Considerations of Load, Velocity, and Material Recruitment

Gear Module Selection on the Basis of Torque

Torque section is one of the important factors in designing a gear module. The torque that is transmitted is proportional to the forces on the teeth of the gear, which increase with a higher transmitted load. Therefore, a larger module is required to maintain equivalent strength and surface durability.

As a general rule of thumb, engineers calculate the torque and power needs first, and then make an initial choice with respect to the module based on what will give enough face width and root strength. Final checks are performed by stress and contact calculations.

If a too small module is selected, tooth bending or surface pitting could occur; if a too big module is adopted, the system will be oversized and overweight, making it costly.

On the Interaction Between Material Strength and Choice of Modules

The selection of the module interacts with material choice in a strong manner. High tensile materials, such as case hardening and alloy steels, can transmit more load with a smaller modulus than softer materials, such as cast iron and plastics.

This sets up a trade-off, where stronger materials allow the gear module to be smaller for a given load-carrying capacity and may reduce the overall assembly footprint while maintaining required torque density and structural integrity. Designers need to balance material properties with module size for an optimal solution.

Wrap Up!

The gear module is far more than a theoretical value; it is the definitive sizing tool that establishes the mathematical relationship between pitch diameter and tooth count; it is essential in the design and application of gears. The module determines the size, strength, pitch diameter, and center distance of the gear. A comprehensive mastery of gear modules is indispensable for engineers and technical procurement specialists alike to ensure system-wide compatibility.

If you are ready to apply the theoretical knowledge of gear modules to your projects and are looking for the right high-quality gears, we invite you to visit JLCMC, where we offer a wide range of precision gears to meet various application needs.

FAQs

How to Convert Module Value to Diametral Pitch?

To convert module value to diametral pitch, use the formula: Diametral Pitch (P) = 25.4 / Module (m), where 25.4 is the conversion factor from millimeters to inches.

How Can I Test the Module of Gear?

The module of a gear may be found by measuring the pitch diameter and dividing it by the tooth count.

Is There a Minimum Number of Teeth per Module?

Yes. For normal pressure angles, there is a minimum number of teeth to prevent undercutting, and this limit is influenced by both module and gear type.